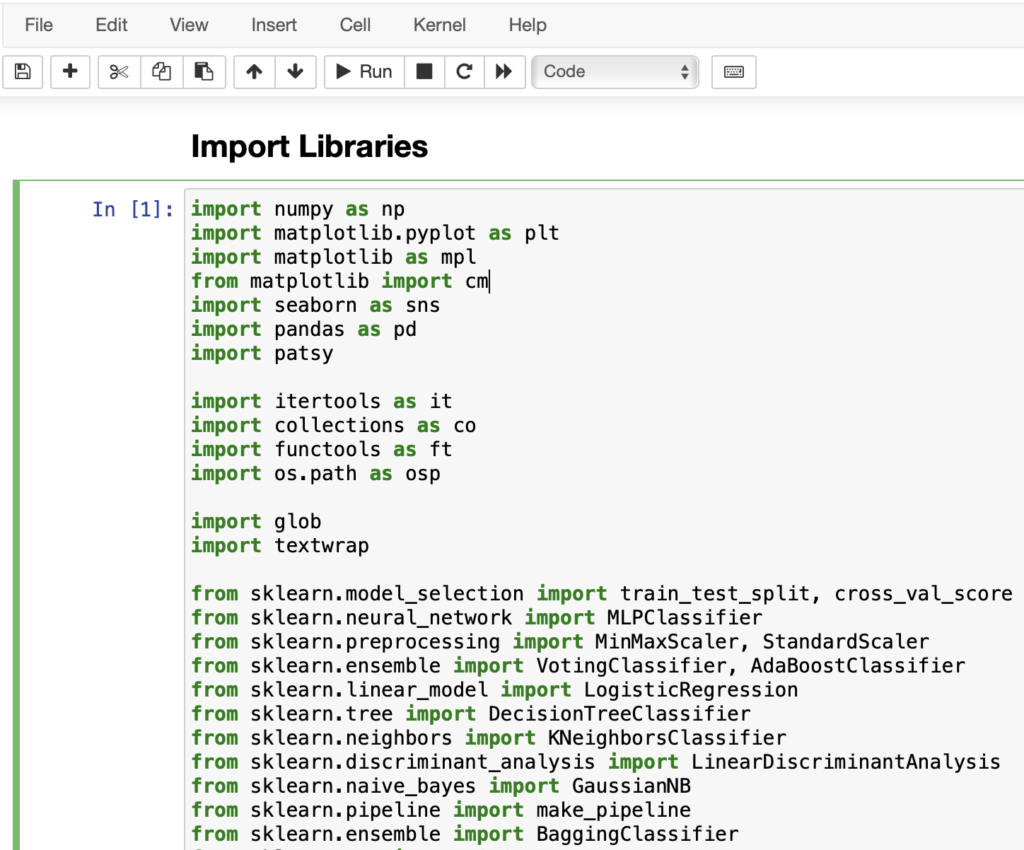
Last week, we looked at languages used for artificial intelligence development. While there are numerous options available, Python has some of the best tools and is the easiest for the beginner to get started with quickly. However, setup can be quite a bit of work. First, setup Python and a development environment – I strongly recommend Jupyter, but VS Code is ok too. Next, begin installing all the necessary libraries – numpy, pandas, and sklearn. You may also wish to install matplotlib and seaborn. When you’ve got all the libraries installed, you can create a block of code in Jupyter to include all the necessary imports in your project such as what I have below. Some of these libraries are large, so you can prune the list to include only the tools you need.
Of particular interest are the sklearn modules. In this section, you will see imports for a variety of different AI algorithms including logistic regression, decision trees, nearest neighbors, linear discriminant analysis, naïve Bayes, and neural networks. These libraries will do the bulk of the work for us with little effort.
Import Libraries
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import cm
import seaborn as sns
import pandas as pd
import patsy
import itertools as it
import collections as co
import functools as ft
import os.path as osp
import glob
import textwrap
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neural_network import MLPClassifier
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.ensemble import VotingClassifier, AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.naive_bayes import GaussianNB
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import BaggingClassifier
from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import f1_score, accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrixLoad Data
The next step for any AI project is to import the data and manipulate as needed
# import the data file from CSV format
data = pd.read_csv(open("data.csv", "rb"))
# show the number of records
recordCount = len(data.index)
print("Record Count: {:d}".format(recordCount))
# optional removal of data
# this will remove all records with a FIELD_VALUE for FIELD_NAME
# data = data.drop(data[data.FIELD_NAME == 'FIELD_VALUE'].index)
# add optional flags for processing
# add a boolean field of true where COLUMN_NAME = VALUE
data.insert(loc=0, column='COLUMN_NAME', value=(data.mood == 'VALUE'))
# show the new record count
newCount = len(data.index)
print("Filtered Count: {:d}".format(recordCount - newCount))
Set Prediction Field & Input Fields
Now that you have loaded the data and manipulated as necessary, it’s time to setup the information for prediction. That will consist of two parts – the field to predict and the values to use for the prediction. So, if I want to determine the value of a house, the prediction value would be the cost and the input fields would include square footage, yard size, number of rooms, etc. In the code snippet below, I will set the fields for predicting home price.
# CSV field to predict
predictionField = 'home_value'
# CSV fields to use for prediction
feature_names = ['square_footage', 'yard_size', 'num_room', 'num_bath']
# extract data into feature set and prediction value (X,y)
X = data[feature_names]
y = data[predictionField]
Split Into Groups
The next important step is to split the data into two groups – training data and test data. The training data will be used by the AI algorithm to ‘learn’ the data. Then, the test data is used to see how well the algorithm actually did in learning the data relationships.
# split into groups
X_train, X_test, y_train, y_test = train_test_split(X, y)
# scale data
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Next Steps
So far, we have loaded the necessary libraries, loaded the data, updated the data to exclude any records we don’t ant, added fields as necessary to augment the data, separated the data into features and prediction fields, and broke the data into groups for training. The next step is where the magic happens – the artificial intelligence algorithm. We’ll look at that next week…